Neste artigo vamos
conhecer mais a fundo os sistemas de numeração, e também aprenderemos como é
realizada a conversão entre eles e ainda além dos números decimais, binários, hexadecimais e octais, também teremos uma introdução aos códigos ASCII, que e uma padronização para os caracteres dos teclados de computadores.
Números
decimais
Números
decimais são os que estamos acostumados a lidar na Matemática convencional.
Também são conhecidos como números de base 10. Isso porque
compreendem dez símbolos numéricos: os números 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
Através
da combinação desses dez números é possível representar todos os números
decimais.
Quando
um número decimal é lido da direita para a esquerda, a primeira posição do
mesmo é representada pelo número 0. A posição do próximo número da esquerda para a
direita é representada pelo número 1 e assim por diante. Por exemplo, vejamos isso
com o número 26802:
O
sistema decimal é baseado em potências de 10. Levando em conta a figura acima
que mostra como é realizada a identificação da coluna do número, em um sistema
decimal cada número é definido pela soma de cada algarismo multiplicado por 10
elevado à potência correspondente à coluna do mesmo:
Agora que vimos uma tabela detalhando
como funcionam os números decimais, vejamos mais alguns exemplos:
E assim por diante...
Números
binários.
Números
binários são os mais importantes em computação. Quando falamos que computadores
atuais são digitais, significa que processam os dados no formato binário.
Números
binários também são conhecidos como números de base 2. Compreendem
somente dois caracteres: o 0 e o 1.
Quando
um número binário é lido da direita para a esquerda, assim como com os números
decimais, sua posição colunar inicial é considerada 0. O próximo dígito mais à esquerda é
considerado de posição 1 e assim por diante, como na figura:
Os
números binários são baseados em potências de 2 e, de forma semelhante aos
números decimais, podem ser definidos pela soma de cada algarismo multiplicado
por 2 (que é a sua base) elevado à potência que corresponde à coluna
correspondente do mesmo:
Para ficar bem claro, seguem mais
alguns exemplos:
Cada
dígito de um número binário é conhecido como bit. Nos exemplos da figura acima temos um
número binário de 4 bits.
Para
mensurar a capacidade de processamento de um computador assim como a capacidade
de armazenamento é utilizado o conceito de byte (representado pela letra B maiúscula).
Um byte equivale
a aproximadamente 8 bits e é representado pela letra bminúscula.
Um bit pode
ser representado somente por duas entidades: ou um dígito 0 ou
um dígito 1.
Um
caracter digitado no teclado tem, aproximadamente, 8 bits.
Quando
falamos que um byte equivale a aproximadamente 8 bits,
estamos tratando da mensuração dos bytes que temos contato no dia-a-dia. Por
exemplo, vejamos uma tabela que relaciona bits e bytes:
|
byte
(B)
|
Correspondência
em bytes
|
bit
(b)
|
Correspondência
em bits
|
Potência
|
|
1
byte
|
1
byte
|
8
bits
|
8
bits
|
20
|
|
1
kB
|
1.024
bytes
|
8
kb
|
8.192
bits
|
210
|
|
1
MB
|
1.048.576
bytes
|
8.192
kb
|
8.388.608
bits
|
220
|
|
1
GB
|
1.073.741.824
bytes
|
8.388.608
kb
|
8.589.934.592
bits
|
230
|
|
1
TB
|
1.099.511.627.776
bytes
|
8.589.934.592
kb
|
8.796.093.022.208
bits
|
240
|
Tabela
ASCII
Os
caracteres que digitamos no teclado, indiferentemente se são letras ou números,
primeiro são convertidos em um código chamado ASCII que
corresponde a um número inteiro decimal. Em seguida são convertidos em números
binários, compostos somente por "zeros" e "uns".
Dessa forma o processador pode realizar os cálculos e retornar um valor.
ASCII
é um acrônimo para American Standard Code for Information Interchange, que em
português significa "Código Padrão Americano para o Intercâmbio de
Informação". Define 128 caracteres, sendo 33 não imprimíveis (utilizados
como caracteres de controle).
Os
caracteres não imprimíveis vão do 1 ao 31, além do 128. Ou seja, os caracteres
imprimíveis vão do 32 ao 126.
Lembra-se
quando vimos os caracteres de "escape"? Vimos, por
exemplo, o"\t". Esses caracteres fazem parte dos caracteres de
controle da tabela ASCII. O "\t" é o caracter 9 na tabela
ASCII, e é um caracter considerado de controle, não imprimível.
Você
pode encontrar centenas de sites na internet que mostram a tabela ASCII
completa.
Números
Hexadecimais
Os
números hexadecimais são conhecidos como de base 16 e são utilizados na
programação de microprocessadores. Oferecem uma forma mais legível para
leitura, e, por isso, são muito utilizados em programação de baixo
nível, por proporcionar uma facilidade em converter um número binário de 4
bits.
Utilizam-se
de dezesseis algarismos, ou dígitos hexadecimais: 1, 2, 3, 4, 5, 6,7, 8, 9, 10, A, B, C, D, E e F.
Os
números hexadecimais têm a capacidade de reduzir uma longa sequência de números
binários em poucos caracteres, pois qualquer combinação de números binários de
4 dígitos pode ser representada por um único símbolo hexadecimal.
Vejamos
uma tabela que compara números decimais, binários e hexadecimais para
realizarmos uma comparação:
|
Decimal
|
Binário
|
Hexadecimal
|
|
0
|
0
|
0
|
|
1
|
1
|
1
|
|
2
|
10
|
2
|
|
3
|
11
|
3
|
|
4
|
100
|
4
|
|
5
|
101
|
5
|
|
6
|
110
|
6
|
|
7
|
111
|
7
|
|
8
|
1000
|
8
|
|
9
|
1001
|
9
|
|
10
|
1010
|
A
|
|
11
|
1011
|
B
|
|
12
|
1100
|
C
|
|
13
|
1101
|
D
|
|
14
|
1110
|
E
|
|
15
|
1111
|
F
|
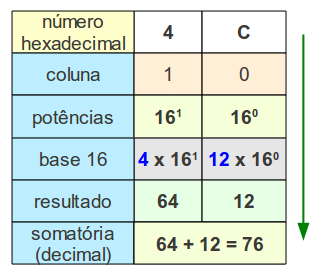
Vejamos uma figura que ilustra a
utilização da base 16 em um número hexadecimal:
Note que o dígito "C" do
número hexadecimal foi substituído pelo seu correspondente (12) na
tabela acima.
Números
Octais
Também conhecido como sistema numérico
de base 8, pois utiliza 8 símbolos numéricos para sua representação: 1, 2, 3, 4, 5, 6, 7 e 8.
Foi muito utilizada em computação para
representar de forma mais suscinta números binários, mas os números
hexadecimais são mais utilizados para esta finalidade nos dias de hoje.
Similar aos números decimais e
binários, utiliza a posição colunar como elemento para determinação do
expoente.
Dessa forma, um número octal segue
normas parecidas com os números decimais e binários no que se refere à
exponenciação:
Vejamos uma tabela comparativa entre
Decimais, Binários, Hexadecimais e Octais:
|
Decimal
|
Binário
|
Hexadecimal
|
Octal
|
|
0
|
0
|
0
|
0
|
|
1
|
1
|
1
|
1
|
|
2
|
10
|
2
|
2
|
|
3
|
11
|
3
|
3
|
|
4
|
100
|
4
|
4
|
|
5
|
101
|
5
|
5
|
|
6
|
110
|
6
|
6
|
|
7
|
111
|
7
|
7
|
|
8
|
1000
|
8
|
10
|
|
9
|
1001
|
9
|
11
|
|
10
|
1010
|
A
|
12
|
|
11
|
1011
|
B
|
13
|
|
12
|
1100
|
C
|
14
|
|
13
|
1101
|
D
|
15
|
|
14
|
1110
|
E
|
16
|
|
15
|
1111
|
F
|
17
|
No próximo artigo vamos aprender a
converter números decimais em binários e vice-versa:
Leia Mais >>